Black-Scholes-Merton期权定价模型(Black-Scholes-Merton Option Pricing Model),即布莱克-斯克尔斯期权定价模型。投资者要想将期权交易工具熟练掌握,对期权定价模型的了解是必不可少的。本文将简述BS–Black-Scholes是啥?如何通俗理解期权定价模型?

一、BS–Black-Scholes是啥?
1997年10月10日,第二十九届诺贝尔经济学奖授予了两位美国学者,哈佛商学院教授罗伯特·默顿(Robert Merton)和斯坦福大学教授迈伦·斯克尔斯(Myron Scholes),同时肯定了布莱克的杰出贡献。
斯克尔斯与他的同事、已故数学家费雪·布莱克(Fischer Black)在70年代初合作研究出了一个期权定价的复杂公式。与此同时,默顿也发现了同样的公式及许多其他有关期权的有用结论。默顿扩展了原模型的内涵,使之同样运用于许多其他形式的金融交易。
布莱克-舒尔斯模型,也称为布莱克-舒尔斯-默顿模型(Black-Scholes-Merton Model),针对无红利流量情况下欧式期权的价值评估,考虑了标的资产评估基准日价值(S)及其波动率(σ)、期权行权价格(X)、行权期限(T)、无风险收益率(r)五大因素以确定期权价值。
期权价格的影响因素很多,基本上来说是一个包含资产价格、到期时间、波动率、行权价格、利率、股息的方程。基本上就是个3-2-1的圣诞树,3个率,2个价格,1个时间,决定了一个方程
y = f(x1, x2, x3, x4, x5, x6)
教科书上是这么写的
V(S,K,σ,T,t,r)其中:V是期权价格S是标的物价格(服从对数正态分布)K是行权价格σ是波动率T是到期日,t是当前时刻,Δt=T-tr是无风险利率。
由于是一个多元函数,所以用泰勒展式展开成偏导的形式,n个一阶偏导,n2个二阶偏导……
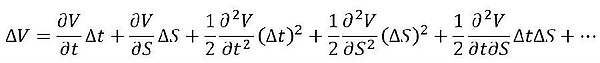
然后就把几个一阶偏导拎出来,做一个定义,就成了所谓的“期权xxxx希腊字母定价法”。
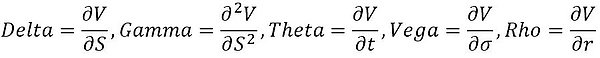
二、如何通俗理解期权定价模型?
众所周知,期权的价值受多种因素的影响。这些因素为标的资产价格、执行价格、波动率、剩余期限和无风险利率。
这些因素如何作用于期权价格的“方向”,想必投资者也都比较清楚,例如剩余期限越少,期权价格会越低;标的资产价格越高,看涨期权价格会越高而看跌期权价格会越低等。
1.但单单知道因素作用的“方向”就够了么?
假设投资者判断标的资产一个星期后会上涨,根据标的资产价格作用的“方向”,他判断出期权价格会涨。根据剩余期限作用的“方向”,他则会得出期权价格要跌。
2.那期权价格到底应该是涨还是跌呢?
要回答这个问题,我们不仅要知道这些因素作用于期权价格的“方向”,还要了解这些因素作用于期权价格“方向”的“速度”。
要知道这个“速度”我们就必须了解期权定价模型。因为模型准确的给出了期权价值和各影响因素的数量化关系。常见的期权定价模型有BSM模型、二叉树模型以及蒙特卡洛定价模型。
关于期权的更多知识,订阅我们下次再见!
白话区块链|同步全球区块链资讯、区块链快讯、区块链新闻
本站所有文章数据来源:金色财经
本站不对内容真实性负责,如需转载请联系原作者
如需删除该文章,请发送本文链接至koinfts@gmail.com

